CG태그를 가진 글들은 당분간 고려대학교 한정현 교수님의 KUOCW 컴퓨터그래픽스 강의록의 내용으로 구성될 예정입니다.- 해당 장의 강의 전체를 담는 형식이 아니라 필자가 그때마다 중요하다고 여겨지는 것들, 팁들 위주로 포스팅됩니다.
- 포스트에 쓰인 이미지들은 고려대학교 한정현 교수님의 강의 ppt에서 발췌되었습니다.
래스터라이저란?
전 포스팅에서 GPU pipeline에서 맨 처음 단계인 vertex shader의 output을 input으로 받는 두 번째 단계이다. 이 단계는 하드웨어로 고정되고 하드웨어가 수행해 준다. 하지만 래스터라이저가 하는 일이 어떻게 이루어지는지 정도는 알아야 fragment shader가 하는 일을 이해하기 편하다.
래스터라이저가 하는 일은 크게 5개로 나누어진다.
- Clipping
- Perspective division
- Back-face culling
- Viewport transform
- Scan conversion
하나씩 간략하게 살펴보도록 하자.
clipping?
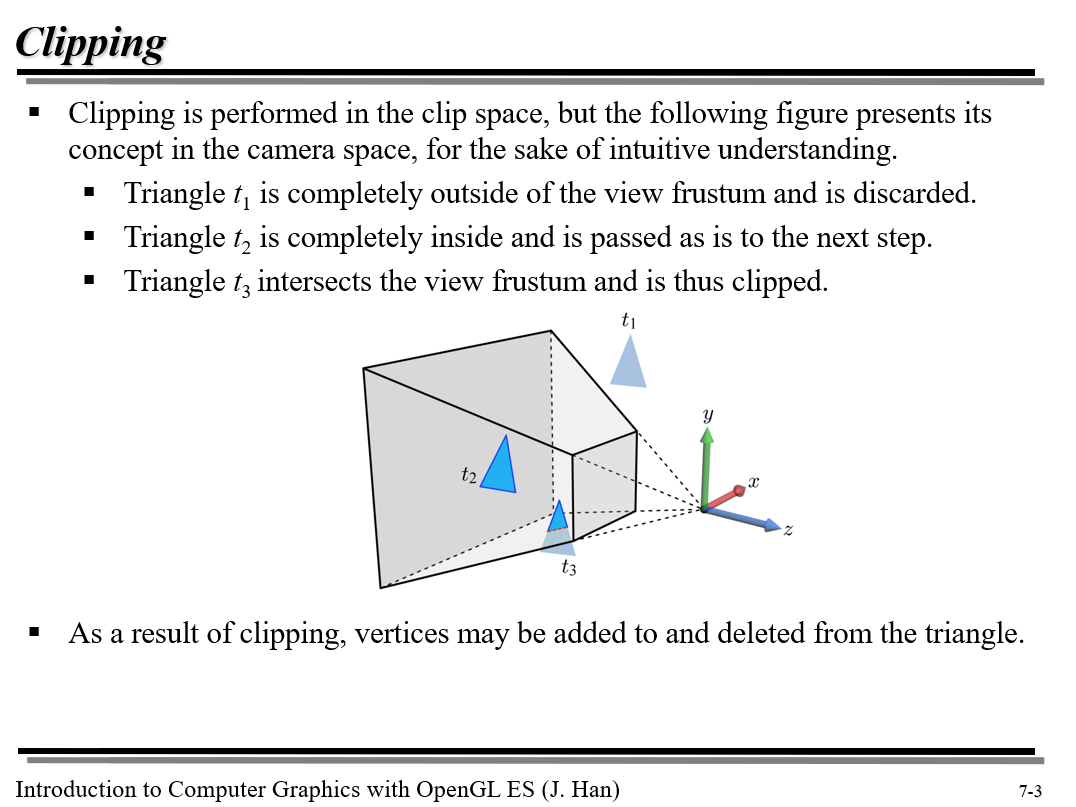
이전 포스팅에서 언급한 view frustum을 투영 변환으로 clip space로 바꾼 다음 공간 경계면 밖으로 일부분이 삐져나오거나 아예 밖에 존재하는 물체들을 clipping(가위치기)하는 작업이다.
그림처럼 일부분이 공간 안에 속하는 경우 (삼각형 t3을 보라) 물체와 경계면이 만나는 선을 따라 새로운 정점을 추가하여 새로운 primitive를 만들어 clipped된다.
Perspective division?
번역하면 ‘원근 나눗셈’이다. 결과론적으로 원근법을 구현하는 단계이다. 투영 행렬 식을 기억하는가?
\begin{pmatrix}
\frac{cot\frac{fovy}{2}}{aspect} & 0 & 0 & 0 \
0 & cot\frac{fovy}{2} & 0 & 0 \
0 & 0 & \frac{f+n}{f-n} & \frac{2nf}{f-n} \
0 & 0 & -1 & 0
\end{pmatrix}
투영 행렬에 동차 좌표를 곱하면 (x',y',z',1)꼴이 되지 않을 수도 있다는 것을 알 것이다. 왜냐하면 변환 후 좌표를 (x',y',z',w')라 한다면 w'는 변환 전 좌표 (x,y,z,w)의 -z이기 때문이다. 따라서 모든 좌표 원소를 -z로 나눠 카테시안 좌표 꼴로 변환하여야 한다.
그런데 생각해 보면 변환 전 view frustum에서 어떤 물체를 이루는 정점들의 좌표가 camera space의 원점에서 z축 반대 방향 쪽으로 멀수록 변환 후 해당 물체의 크기는 상대적으로 더 작아지는 것을 알 수 있다. 왜냐하면 변환 전 z좌표 값에 -을 붙인 -z으로 전체 좌표를 나누기 때문이다.
아래 그림의 선분 $l_{1}$, $l_{2}$를 보면 변환 전 두 선분은 길이가 똑같지만 변환 후 l_{1}이 l_{2}보다 길이가 짧아져 결국 카메라로부터 멀리 있던 l_{1}가 더 작게 보이는 효과, 즉 원근법을 볼 수 있다.
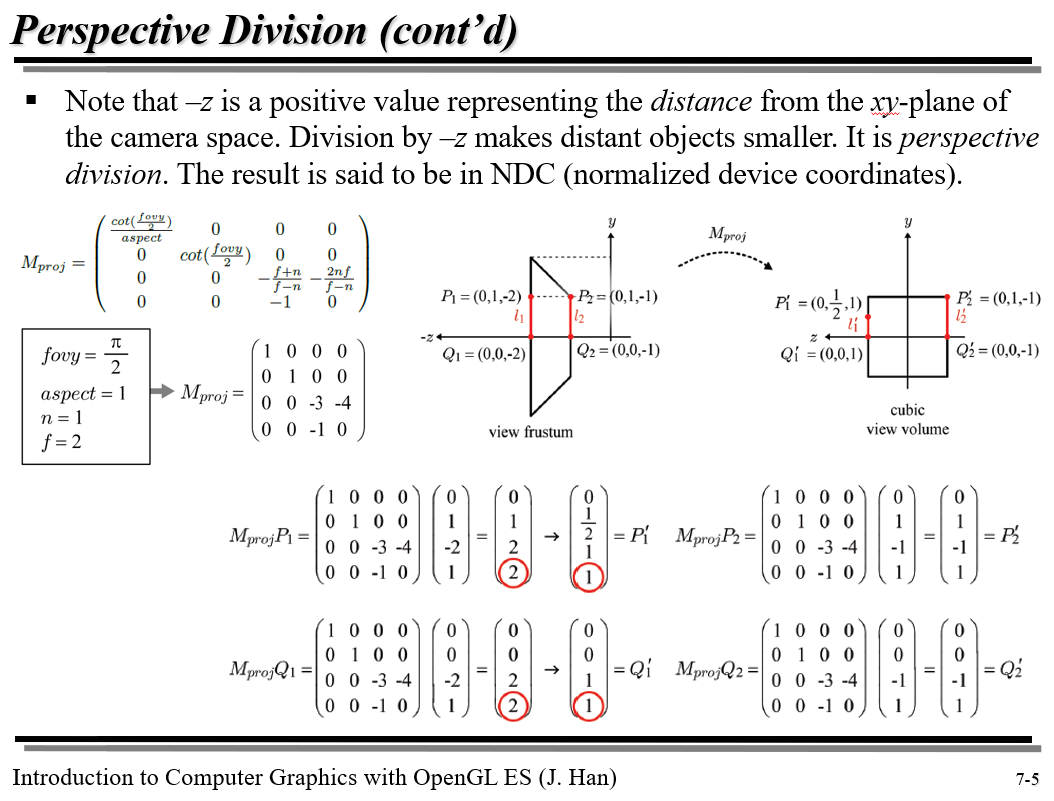
추가로, Perspective division으로 얻은 카테시안 좌표를 NDC(normalized device coordinates)로 일컫는다. normalized가 들어가는 이유는 카테시안 좌표의 x,y,z의 범위가 모두 [-1,1]이기 때문이다.
Back-face culling?
개인적으로 래스터라이저가 하는 일의 꽃이라고 생각한다.
이 단계는 우리가 실제 사물을 보는 것처럼 뒷면 쪽을 display에 올리지 않거나 반투명한 재질의 경우 앞,뒤면을 살짝씩 보이게 하는 등 처리를 하는 단계이다. 보통은 투명하지 않은 재질을 가진 물체를 많이 구현하므로 뒷면이 보이지 않게 display에 올리지 않는 구현을 많이 선택한다.
우리가 화면을 볼때 어떤 물체의 앞,뒷면을 판단하는 건 쉽다. 하지만 어떻게 컴퓨터가 이게 앞면인지 뒷면인지 판단하게 할까?
내적(inner product)으로 접근해보자. 원래 clip space에서 설명되어야 하지만 설명을 단순화하기 위해 view frustum에서 설명하겠다.
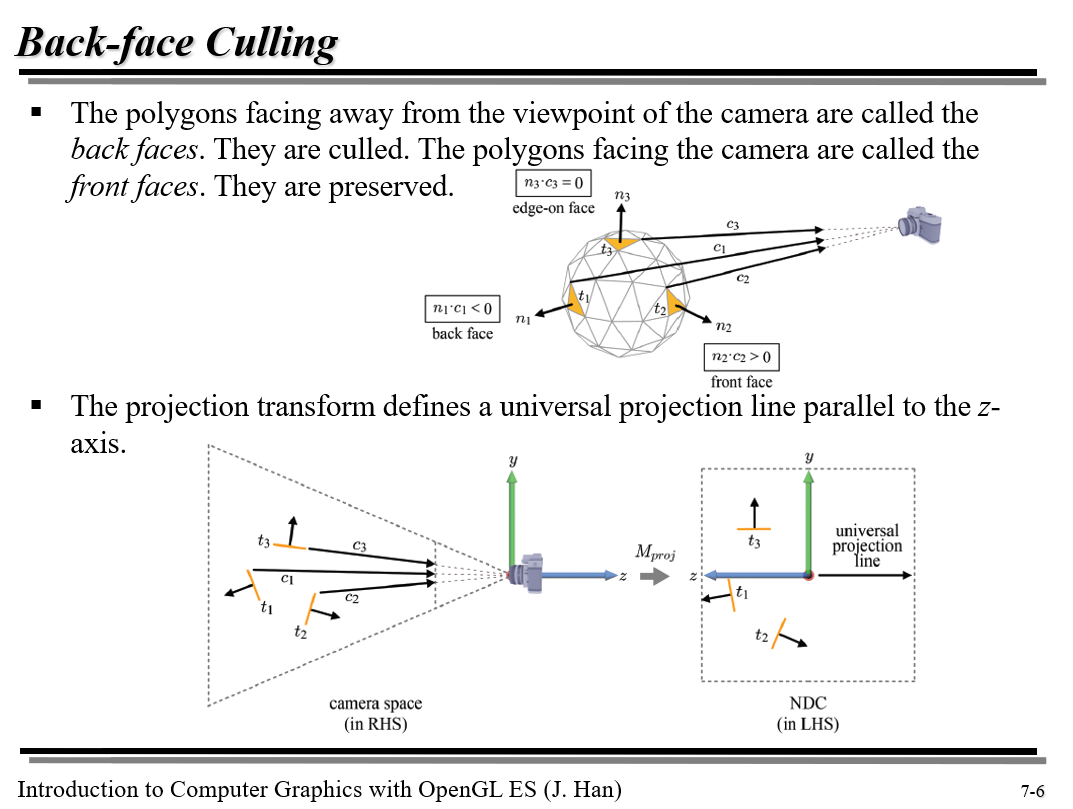
$n_{1}$, $n_{2}$, $n_{3}$은 각 삼각형의 normal vector이고
$c_{1}$, $c_{2}$, $c_{3}$은 각 삼각형의 한 정점과 camera space의 원점 EYE를 이은 벡터이다. 이것들은 투영선들의 일부다.
우리는 벡터 a,b의 inner product의 공식이 $\Vert a \Vert \Vert b \Vert cos\theta$임을 안다. $cos\theta$는 $\theta$의 값이 $\frac{\pi}{2}$가 넘어가면 음수로 가는 그래프이다.
따라서 삼각형 $t_{1}$처럼 뒷면인 삼각형 mesh의 normal vector가 $c_{1}$과 이루는 각이 둔각이므로 내적은 음수가 되고, 예각은 앞면, $t_{2}$처럼 직각을 이루는 것은 변만 보이는 삼각형임을 알 수 있다.
잠깐! 삼각형 & 정점 normal?
정점 normal과 삼각형 normal을 구하는 방법을 review하고 넘어가자.
* 삼각형 normal
삼각형을 이루는 벡터 $v_{1}$, $v_{2}$를 구해 두 벡터의 벡터곱(outer prodect - 외적)을 구한다. 이때 정점들이 반시계(CCW)방향으로 정렬되어 있어야 물체 표면 바깥쪽으로 normal vector의 방향이 정해진다.


* 정점 normal 그 정점을 포함하는 삼각형들의 normal vector를 평균내어 구한다.
다시 돌아와서..
근데 사실 내적을 할 필요도 없다. clip space로 변환되면 투영선이 나란히 평행하게 되는데 이때 삼각형 mesh들을 xy평면으로 투영시키자. xy평면을 우리가 볼 스크린이라고 생각하면 편하다.
위에서 말한 대로 삼각형 정점들이 반시계(CCW)방향으로 정렬되어 있다고 가정하고 xy평면 입장에서 바라볼 때 그 정렬 방향이 반시계로 유지되면 앞면이고, 시계로 바뀌어 버리면 뒷면이 된다.
이렇게 되는 이유는 지난 단계에서 삼각형 vertex들을 반시계 방향으로 정렬하고 normal vector를 설정할 때는 물체 바깥 시점에서 설정했지만 그것들을 clip space에서 xy평면에 투영시키면 뒷면의 경우는 결국 물체 안쪽에서 바라보는 시점이 되어버리는 것이기 때문이다.
이해가 안간다면 그림을 보고 이해해보자.

이제 이 질문에 답할 때가 왔다.
우리가 화면을 볼때 어떤 물체의 앞,뒷면을 판단하는 건 쉽다. 하지만 어떻게 컴퓨터가 이게 앞면인지 뒷면인지 판단하게 할까?
행렬식을 사용한다. xy평면에 투영된 삼각형 하나를 생각하고 각 정점 $v_{i}$의 좌표는 $(x_{i}, y_{i})$라 하자. 삼각형 normal vector를 구할 때처럼 삼각형의 정점 $v_{1}$, $v_{2}$, $v_{3}$가 존재할 때 (이 세 정점은 normal vector를 설정할 때 반시계 방향으로 정렬되었었다.) $v_{1}$, $v_{2}$를 잇는 벡터 $(x_{2}-x_{1}, y_{2}-y_{1})$과 $v_{3}$, $v_{1}$를 잇는 벡터 $(x_{3}-x_{1}, y_{3}-y_{1})$을 생각하고 행렬식을 계산한다.
\[\begin{array}{|cccc|} (x_{2}-x_{1}) & (y_{2}-y_{1})\\ (x_{3}-x_{1}) & (y_{3}-y_{1}) \end{array} = (x_{2}-x_{1})(y_{3}-y_{1}) - (x_{3}-x_{1})(y_{2}-y_{1})\]이 결과가 음수면 뒷면, 양수면 앞면을 나타낸다.
Viewport transform?
이제는 clip space에서 우리가 보는 윈도우 화면으로 옮길 시간이다. 우리가 보는 공간을 윈도우 공간이라고 일컫는다.
우리가 보는 화면은 2차원일지 몰라도 이 변환의 종착지인 윈도우 공간은 3차원이다. 그래서 이 윈도우 공간의 property는 다음과 같다.
- minX
- minY
- w
- h
- minZ
- maxZ
$(minX, minY)$는 정면에서 바라볼 때 왼쪽아래 점의 좌표이다.
w, h는 각각 윈도우 화면의 width, height를 나타낸다.
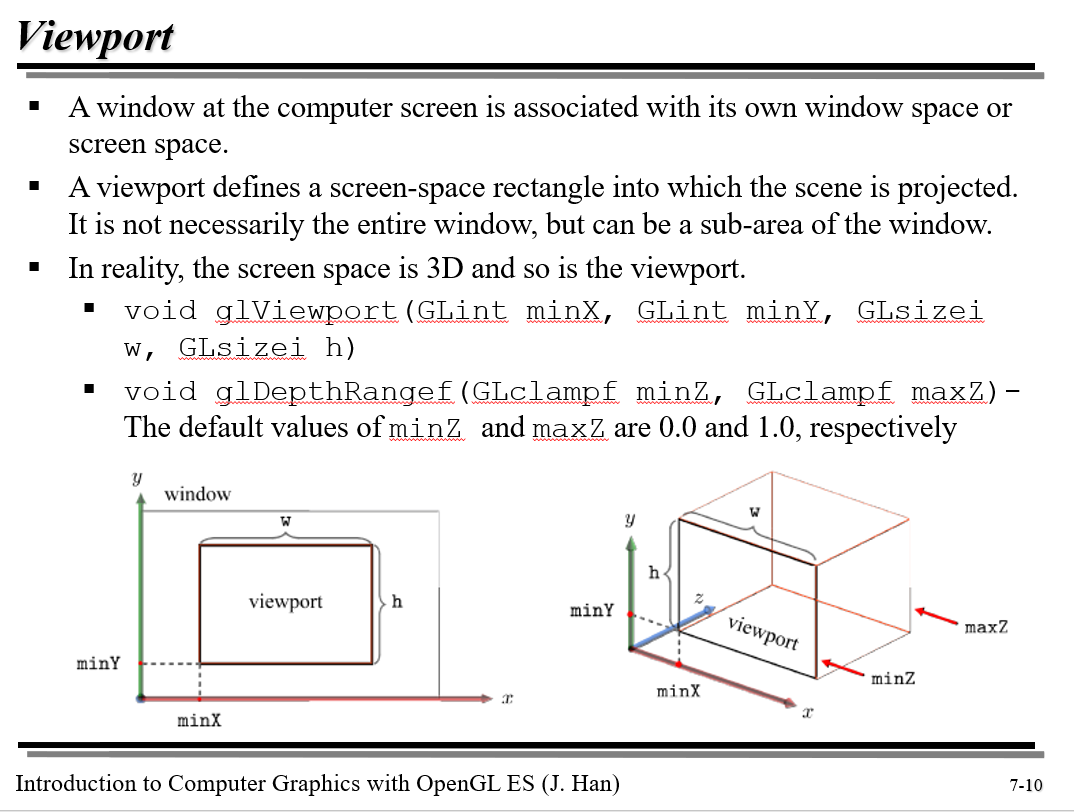
clip space에서 window space(screen space)로 넘어갈 때는 확대와 이동이 모두 사용된다. 이때 쓰이는 scaling은 uniform하지 않으므로 normal을 변환할 때는 바로 갖다박으면 안 된다. 아직 배우진 않았지만 똑같이 $M^{-T}$로 하지 않을까?
하여튼 viewport transform의 행렬은 다음과 같다.
\[\begin{pmatrix} \frac{w}{2} & 0 & 0 & minX + \frac{w}{2} \\\ 0 & \frac{h}{2} & 0 & minY + \frac{h}{2} \\\ 0 & 0 & \frac{maxZ-minZ}{2} &\frac{maxZ+minZ}{2} \\\ 0 & 0 & 0 & 1 \end{pmatrix}\]행렬식의 유도는 간단하다. 그림을 보면 이해 가능하다. 변환할 스크린 공간의 property가 뭔지 생각하면 쉽다.
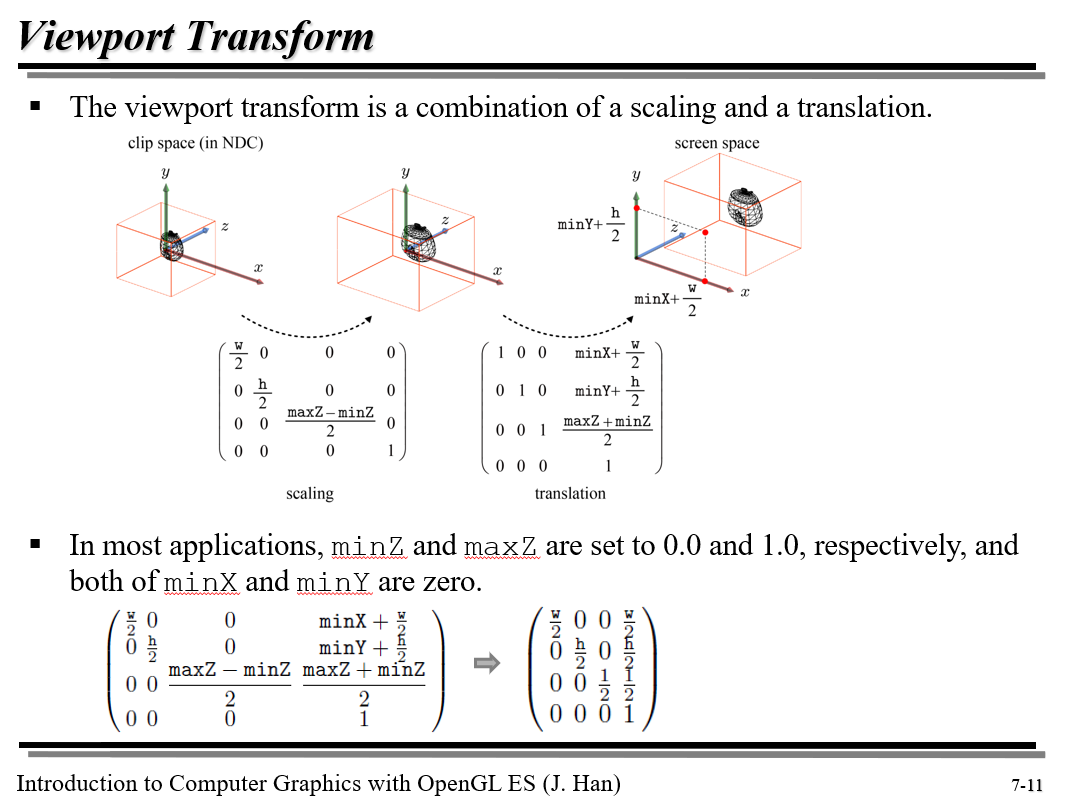
-
scaling : 222 정육면체를 직육면체
윈도우 공간(=스크린 공간)으로 scaling한다. 각 변의 절반이 1 -> w/2, h/2, (maxZ-minZ)/2로 각각 바뀜을 알 수 있다. -
moving transform : 원점을 이동시킨다. 스크린 공간의 왼쪽 아래 앞쪽 점의 좌표가
$(minX, minY, minZ)$가 되게 해야 한다는 것을 기억하자.
Scan conversion?
viewport transform이 삼각형 mesh들을 스크린 공간으로 옮기는 변환이라는 것을 이해했을 것이다.
Scan conversion에서는 삼각형 내부 프래그먼트(fragment)를 생성할 것이다.
래스터라이져가 받는 input은 vertex shader가 생성하는데 크게 세 가지가 있다.
- vertex transform - 3차원
- vertex normal - 3차원
- vertex texture coord(좌표) - 2차원
이 중에 texture coord는 vertex shader가 별다른 처리를 하지 않는다.

이제 이에 대한 처리를 이 단계에서 수행할 것이다. 보간이다.(interpolation)
우리가 보는 스크린 화면은 픽셀로 이루어져 있고 수평 방향으로 이어진 스크린 픽셀들을 scan line이라고 한다.
삼각형을 예로 들어보자. 실제로는 texture coord를 보간하는 것이지만 여기서는 쉬운 예를 위해 color를 보간하는 것으로 갈음하였다.
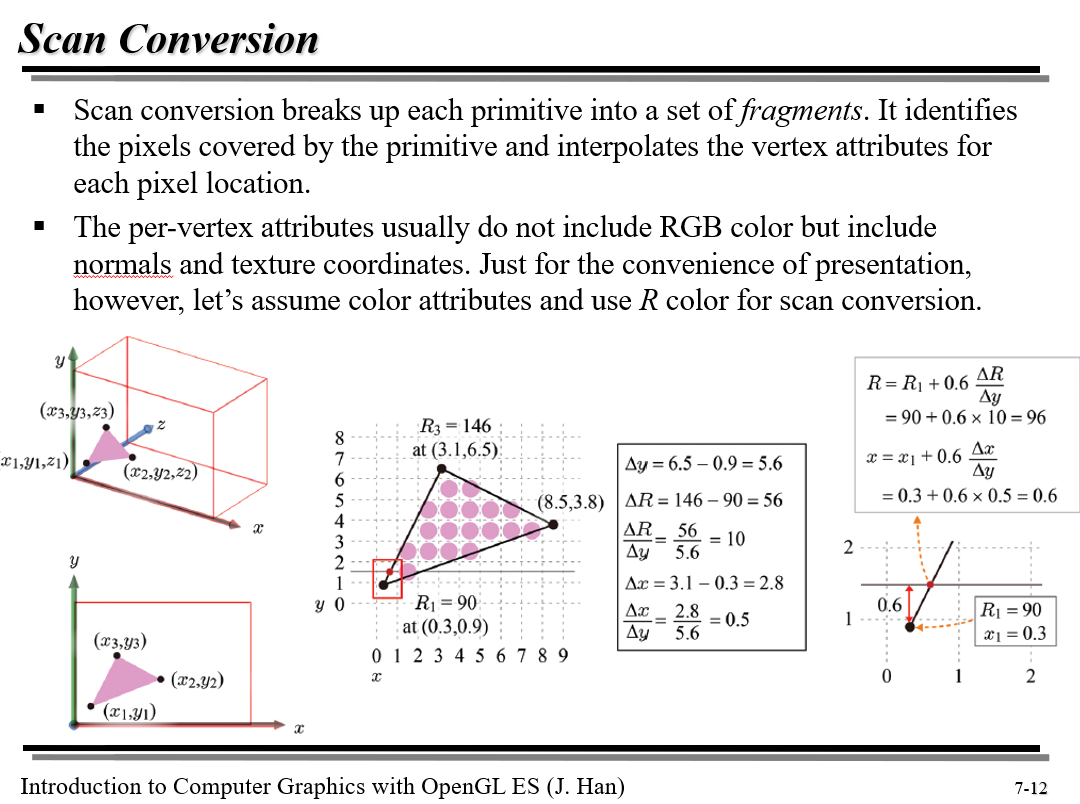
R은 그 점이 가지는 color의 수치적 표현이다. scan line의 좌표는 x.5의 수치를 갖는다.
(ex : (1.5,3.5)) 즉, 픽셀의 정중앙이다.
네모 박스 안 변화율들은 y, R, x의 변화율이다.
- 전제 조건 : 삼각형의 세 점에 대해서 (x,y)좌표 값,
R수치를 알고 있다.
여기서는 겹선형보간(bilinear interpolation)을 사용한다. 어떻게 수행되냐면
-
삼각형의 변을 따라 선형 보간(linear interpolation)을 만나는 scan line에 대해 수행한다.
-
삼각형의 테두리 scan line에 대해서는
y,R,x을 알고 있으므로 이번에는 x축에 평행한 가로줄을 여러 개 그어 그scan line에 속하는 픽셀들에 대해 선형 보간한다.
즉, 테두리에 대해 먼저 보간하고 그 다음 내부에 대해 한 가로줄씩 보간하는 것이다.
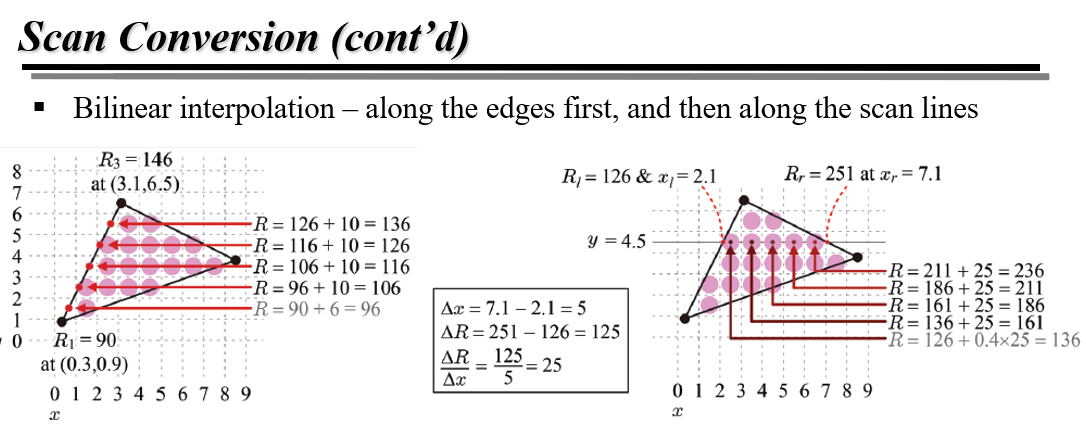
위에서는 tex coord에 대해서만 언급했지만 사실 vertex normal도 같은 방식으로 보간된다.
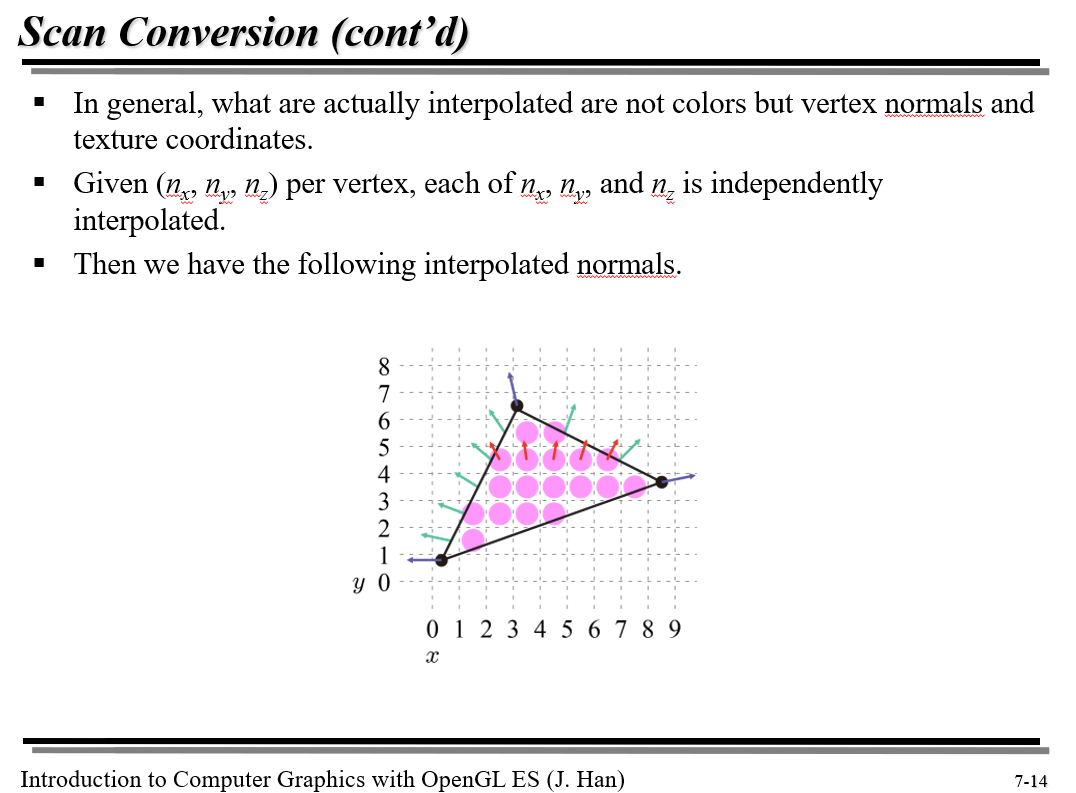



댓글남기기