쿼터니언이 뭘까?

• CG 태그를 가진 글들은 당분간 고려대학교 한정현 교수님의 KUOCW 컴퓨터그래픽스 강의록의 내용으로 구성될 예정입니다.
• 해당 장의 강의 전체를 담는 형식이 아니라 필자가 그때마다 중요하다고 여겨지는 것들, 팁들 위주로 포스팅됩니다.
• 포스트에 쓰인 이미지들은 고려대학교 한정현 교수님의 강의 ppt에서 발췌되었습니다.

---

사실 포스팅 순서가 이상하다는 것을 알 것이다. 하지만 이 블로그는 내 개인 공부에서 부족하거나 특별히 눈에 띄는 점들 위주로 포스팅하는 목적으로 만들어진 블로그이고 건너뛴 chapter들은 내가 나중에 간략하게라도 정리를 할 생각이니 안심하기 바란다. 사실 찾는 사람도 없을 것 같긴 한데ㅋㅋ

Quternion(쿼터니언)이란?

Quternion이란 뭘까? 난 이 단어를 unity에서 게임을 만들 때 처음 접했다. 강의를 따라 게임을 만들어 보는 것이었는데, 3인칭 rpg 게임이었다. 여기서 3인칭 카메라 움직임을 구현할 때 썼었던 기억이 난다. 캐릭터가 회전하면 같이 카메라 시점도 돌아야 해서 lerp()함수와 같이 사용하면서 뭣도 모르고 썼었다.

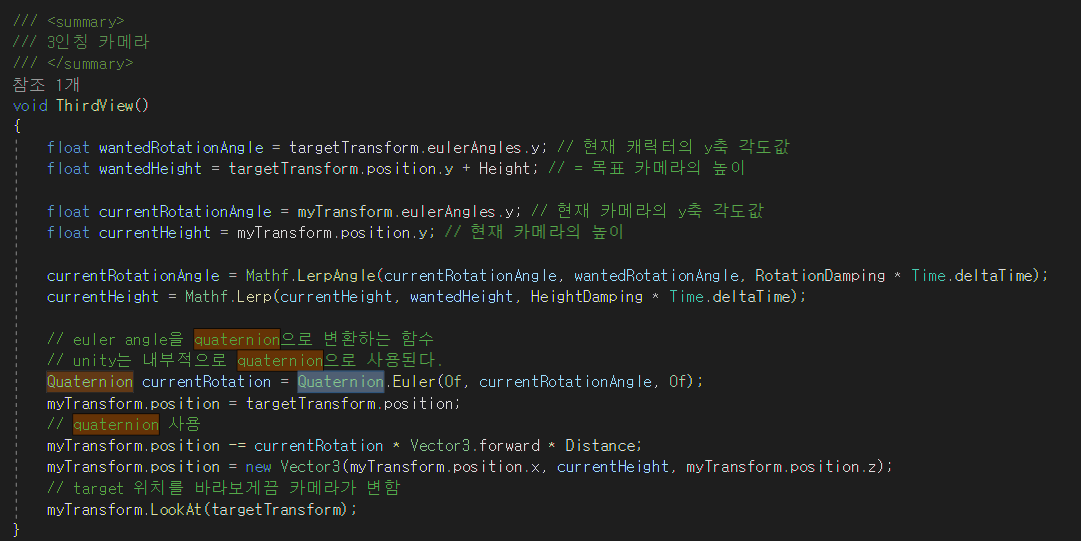
쿼터니언을 한 문장으로 요약하자면 openGL, Unity 등에서 임의의 방향이나 회전을 회전을 나타내는 데 쓰이는 형식이다.

본격적으로 소개하기 전에 우리에게 친숙한 개념인 오일러 변환(Euler transform)을 생각해 보자.
오일러 변환은 chapter 04에 소개되었던 주축(x,y,z축)을 중심으로 한 회전을 결합하여 전체 회전을 표현하는 방법이다. 이렇게 표현할 시 세 축 중심의 회전각 $\theta_{1}, \theta_{2}, \theta_{3}$을 오일러 각이라고 부른다.

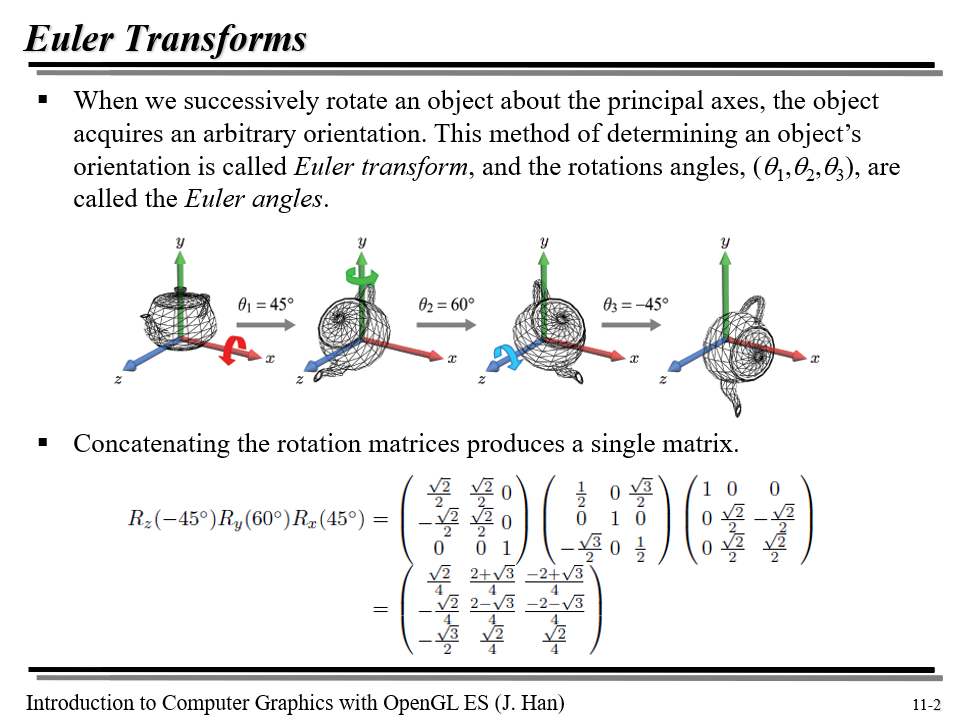
위 그림에서 한 회전을 나타낼 때 z축으로 -45도, y축으로 60도, x축으로 45도의 오일러 각 순으로 순서대로 각 주축에 대해 회전함으로써 나타내는 것을 알 수 있다. 각 주축에 대한 회전 행렬은 chapter 04에 소개되었다.

위 그림에서 알 수 있듯이 오일러 변환 행렬의 크기는 $3 \times 3$이다. 반면에 쿼터니언은 복소수 개념을 확장한 것으로 네 개의 항으로 구성된다.

\[(q_{x}, q_{y}, q_{z}, q_{w}) = q_{x}i + q_{y}j + q_{z}k + q_{w}\]

$q_{x}, q_{y}, q_{z}$는 허수부라고 하고, $q_{w}$는 실수부라고 한다. i,j,k는 허수단위이며, 일반 허수와 같이 $i^{2} = j^{2} = k^{2} = -1$라는 성질을 가진다. 특이한 것은 다음과 같은 순환치환적인 특징을 가진다.

\[ij = k, ji = -k \\ jk = i, kj = -i \\ ki = j, ik = -j\]

여기서 쿼터니언을 결합한 결과는 쿼터니언이 된다는 것을 미리 언급한다. 그러면 두 쿼터니언 p, q를 결합한 쿼터니언 $pq$를 생각하면 $pq \neq qp$라는 것을 알 수 있다. 즉, 쿼터니언의 곱셈에 대해 교환법칙이 성립하지 않는다. 이에 대한 설명을 뒤에서 다시 언급하겠다.

또, 쿼터니언을 계산했으면 이 결과를 해당 차원의 좌표로 변환해야 써먹을 수 있을 것이다. 쿼터니언은 보통 3차원 회전을 나타낼 때 많이 쓰이지만 2차원 회전도 살펴보면,
실수부 부분과 허수부 부분이 각 x,y좌표가 되고 3차원은 허수부 부분의 i,j,k의 계수가 각 x,y,z좌표가 된다.

언뜻 보면 왜 오일러 각을 놔두고 쿼터니언이라는 요상한 것을 써야 하는지 이해가 가지 않는다. unity 엔진도 그렇고 왜 오일러 각을 놔두고 이런 걸 쓰는 것일까?

쿼터니언의 장점은 다음과 같다.

• 보간 결과에 오류가 없다.
• 주축 회전이 아닌 임의의 축에 대해 계산이 편하고 직관적이다.

보간 결과에 오류가 없다?

오일러 변환은 주축에 대한 회전을 결합하여 회전을 나타낸다는 점에서 쿼터니언보다 직관적일지 몰라도 한 가지 단점이 있는데, 변환 간 보간 결과가 일치하지 않는다는 점이다.

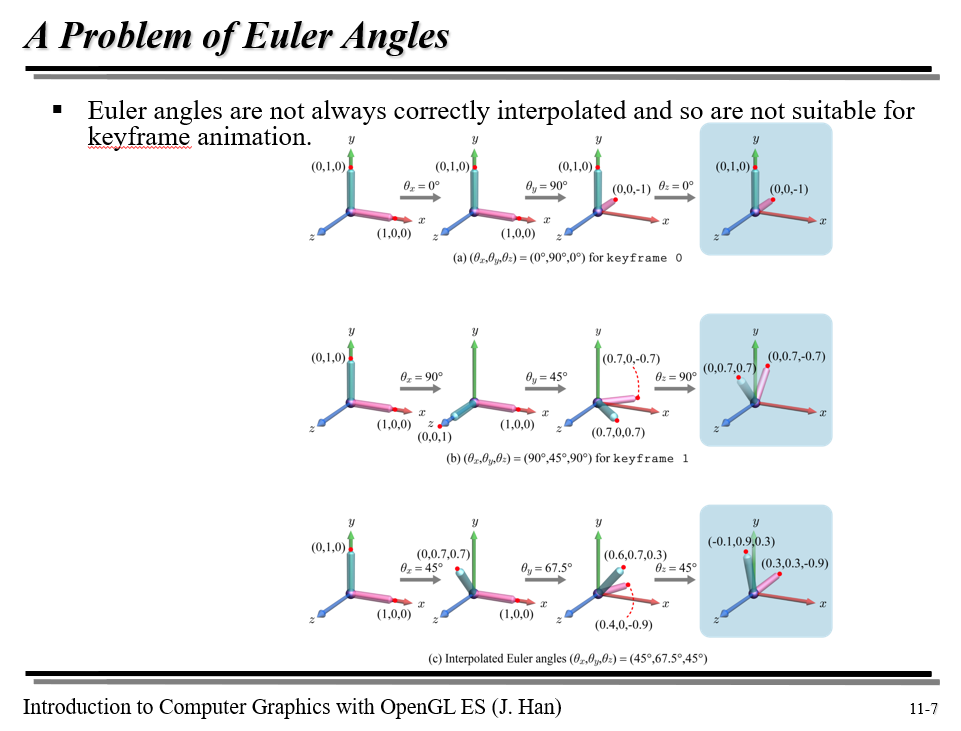
그림들을 행 단위로 보자. 모든 행은 오일러 변환인데, x축으로 0도, y축으로 90도, z축으로 0도 변환한 것이고 2행은 x축으로 90도, y축으로 45도, z축으로 90도 변환한 것이다. 3행은 각 주축에 대한 변환을 1행과 2행 사이에서 딱 중간($t=\frac{1}{2}$)에서 보간한 것이다. 즉, x축으로 $\frac{(0+90)}{2}$도, y축으로 $\frac{(90+45)}{2}$도, z축으로 $\frac{(0+90)}{2}$도 회전한 결과이다.

그런데 우리의 예상과 결과가 다르다. 1행과 2행의 오일러 변환을 각 축 오일러 각 사이 딱 절반으로 보간했으니까 결과도 1행과 2행의 중간이 되어야 하는데 그렇지 않다. 심지어 1행, 2행 모두 yz평면에 있는데 3행은 그렇지도 않다. 보간 결과가 일치하지 않는다.

반면 쿼터니언은 보간 결과에 오류가 없다. 대신 보간 방법이 더 복잡하다. 회전을 나타내는 두 개의 단위 쿼터니언 $q,r$을 생각하면

\[\frac{sin(\phi(1-t))}{sin\phi}q + \frac{sin(\phi t)}{sin\phi}r\]

로 보간된다. $\phi$는 4차원 단위 구체 상에서의 $q, r$사이의 각도이다. $t$는 보간 매개변수이다(0~1로 정규화).

q와 r을 내적시키면 내적 공식을 이용하여 $\phi$를 알 수 있고 따라서 $sin(\phi)$이나 기타 값들을 알 수 있어 공식을 계산할 수 있다.
내적 공식은 $\Vert q \Vert \Vert r \Vert cos\phi$인데 q와 r의 길이가 단위 쿼터니언이므로 1이 되어서 $cos\phi$가 된다.
또다른 내적 공식은 벡터를 내적하듯이 각 쿼터니언의 성분을 곱한 것의 합이므로 두 결과를 $=$로 연결하고 각 좌항, 우항에 $arccos$(코사인의 역함수)를 곱해주면 $\phi$를 알 수 있다.

(1)의 증명 과정은 구체 선형보간이라는 것을 이해해야 한다. 본문 p.193에 언급된다.

추가로, 오일러 각이 전체 회전의 내용은 같더라도 어떤 주축에 대한 회전을 먼저 수행하냐에 따라 결과가 달라지는 것처럼 쿼터니언도 앞에서 언급하였듯이 쿼터니언의 곱셈에 대해 교환법칙이 성립하지 않으므로 전체 쿼터니언 성분은 같더라도 어떤 쿼터니언을 먼저 곱하냐에 따라 결과가 달라질 수 있다.

임의의 축에 대한 계산이 직관적이다?

3차원 벡터 p를 임의의 축 u 중심으로 $\theta$만큼 회전시키는 경우를 생각하자. 이것에 관해 논하려면 먼저 회전할 벡터와 회전 변환 각각을 쿼터니언으로 표현하는 방법에 대해 알아야 한다.

3차원 벡터를 쿼터니언으로 나타내는 법

3차원 벡터 p = $(p_{x}, p_{y}, p_{z})$를 쿼터니언으로 변환하면 아래와 같이 허수부가 p가 되고 실수부는 0이 된다. 쿼터니언 변환 결과는 $\mathbf{p}$로 표기한다.

\[\mathbf{p} = (p_{x}, p_{y}, p_{z}, p_{w}) = ({p}_{v}, p_{w}) = (p,0)\]

임의의 축을 중심으로 하는 3차원 회전 변환을 쿼터니언으로 나타내는 법

3차원 상의 임의의 축을 벡터로 나타내 보자. 축 상의 아무 점이나 잡고 벡터를 만든 다음 벡터의 길이로 나눠주면 해당 축의 방향을 가진 단위 벡터 $\mathbf{u}$가 완성된다.

이제 이 단위 벡터 $\mathbf{u}$ 중심으로 $\theta$만큼 도는 회전 변환을 쿼터니언 $\mathbf{q}$로 나타내면 된다.

\[\mathbf{q} = (\mathbf{q}_{v}, q_{w}) \\ = (sin\frac{\theta}{2}\mathbf{u}, cos\frac{\theta}{2})\]

$sin\frac{\theta}{2}\mathbf{u}$는 쿼터니언 $\mathbf{q}$의 허수부이며 이는 $i, j, k$로 이루어져 있고 각 계수에 단위벡터 $\mathbf{u}$의 각 성분을 넣어주면 된다.

$\mathbf{u} = (u_{x}, u_{y}, u_{z})$일때

\[\mathbf{q} = (sin\frac{\theta}{2}\mathbf{u}, cos\frac{\theta}{2}) \\ = (sin\frac{\theta}{2}u_{x}, sin\frac{\theta}{2}u_{y}, sin\frac{\theta}{2}u_{z}, cos\frac{\theta}{2})\]

가 된다.

이렇게 변환된 회전 쿼터니언 $\mathbf{q}$를 쿼터니언 $\mathbf{p}$에 적용시키면

\[\mathbf{p}^{\prime} = \mathbf{q}\mathbf{p}\mathbf{q}^{*}\]

가 된다. $\mathbf{q}^{*}$는 $\mathbf{q}$의 켤레복소수이다. 켤레복소수는 허수부의 부호를 바꾼 것이다.

\[\mathbf{q}^{*} = -q_{x}i - q_{y}j - q_{z}k + q_{w}\]

이처럼 쿼터니언으로 임의의 3차원 축에 대한 회전을 나타내는 방법은 간단하지만 오일러 변환은 그에 비해 어렵다는 것을 알 것이다. 오일러 변환은 각 주축 x,y,z에 대해 변환을 순서대로 거쳐야 하고 임의의 축에 대한 정보를 안다 할지라도 바로 변환하기가 어렵다.

쿼터니언을 사용한 보간 방법은 구체 선형보간으로, 앞에서 언급하였다.

쿼터니언과 회전 행렬 사이의 변환

여기쯤에서 unity와 같은 게임 엔진에서 쿼터니언이 내부적으로 어떻게 사용되는지를 짚고 넘어갈까 한다.

1. 게임엔진 사용자가 물체를 임의의 축 $u$에 대해 회전시키는 명령을 내린다.
2. 물체를 이루는 다각형 mesh들의 vertex coordinate들(vector)이 쿼터니언으로 변환된다.
3. 그 쿼터니언들과 $u$를 변환한 쿼터니언이 결합되어 회전을 한다.
4. 변환된 결과 쿼터니언을 다시 3차원 vertex coordinate(vector)로 변환되어 엔진 inspector에 표시된다.

지금까지 배운 내용과 경험을 바탕으로 써본 거라 다소 정확하지 않을 수 있다. 하튼 엔진 내에서는 이와 비슷하게 진행될 것이다.

여기서 3번을 보자. 쿼터니언과 쿼터니언을 곱할 때는 당연히 쌩으로 곱할 수 없다. 3차원을 표현하는 쿼터니언의 경우 dimension이 $4 \times 1$이기 때문이다. 그래서 내부적으로 곱할 때는 회전 쿼터니언을 회전 행렬로 바꿔서 곱한다.

위 행렬이 쿼터니언 \(\mathbf{q} = (q_{x}, q_{y}, q_{z}, q_{w})\)를 회전 행렬로 바꾼 결과이다.

반대로 회전 행렬을 쿼터니언으로 바꿀 수도 있다.